Recorriendo un laberinto

El diario El País publicó ayer un problema muy interesante de recorrido de un laberinto:

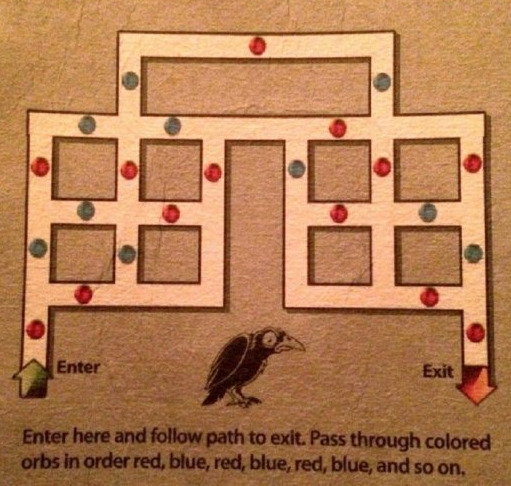
La consigna dice: «Entre aquí, y siga el camino hacia la salida. Pase a través de las esferas en orden rojo, azul, rojo, azul, rojo, azul y así sucesivamente». Lo usual cuando alguien se enfrenta a este tipo de problemas, es que intente -como quien realmente entra físicamente a un laberinto- recorrer distintos caminos, volviendo hacia atrás uno o más pasos al encontrarse que por el actual no puede llegar a la salida. Vamos a analizar una forma bastante interesante de resolverlo, utilizando distintas estrategias y viendo a dónde nos conduce cada una. (Aunque sería útil que primero dedicara unos minutos a intentar resolverlo).

Una aclaración se hace necesaria: cuando el enunciado dice «pase a través de las esferas», significa que no se puede «tocar» una esfera y retroceder, sino que debe pasarse sobre ella, quedando del otro lado (siendo imposible volver directamente por el mismo camino, ya que se repetiría el color).

Análisis bottom-up

Esta estrategia de análisis («bottom-up», «ascendente» o «de abajo hacia arriba») consiste en examinar el objetivo y buscar el último paso necesario para llegar a él. En el caso de nuestro laberinto, este es obvio:

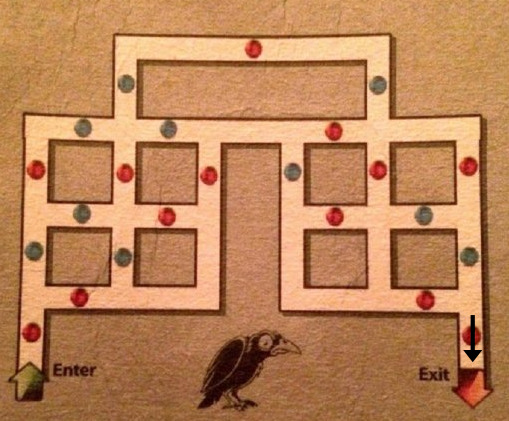
Esto es: para salir del laberinto, debemos atravesar la esfera roja en el sentido que marca la flecha. Ahora, nos preguntamos nuevamente: ¿qué paso podemos realizar para llegar a esto? Puesto que la última esfera es roja, la anterior debe ser azul. Nuevamente, no tenemos más que una opción:

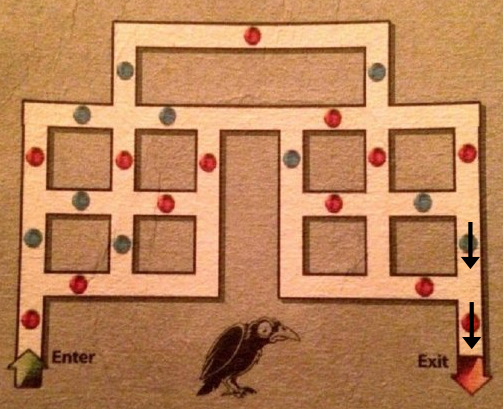
Nuevamente nos preguntamos: ¿cómo podemos llegar hasta aquí? Evidentemente, pasando por la única esfera roja que antecede a la azul que hemos cruzado:

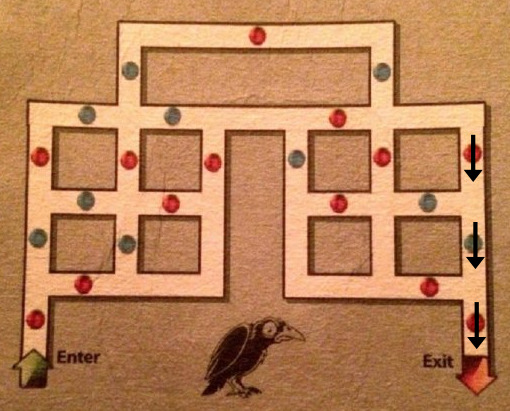
Vamos a abreviar algunos pasos, ya que en todos ellos la esfera anterior de distinto color es única. Razonando de esta forma llegamos a la siguiente situación:

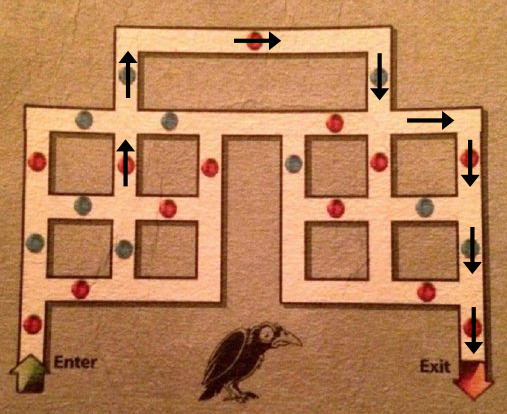
¿Qué sabemos hasta aquí? Que cualquiera sea el recorrido que hagamos dentro del laberinto, para salir de él deberemos seguir el trayecto marcado por las flechas. ¿Y cómo podemos llegar a esta situación? Encontramos que esta vez no hay una única esfera azul que anteceda a la roja que inicia el trayecto, sino dos. Entonces, claramente, las únicas dos posibilidades son las siguientes:

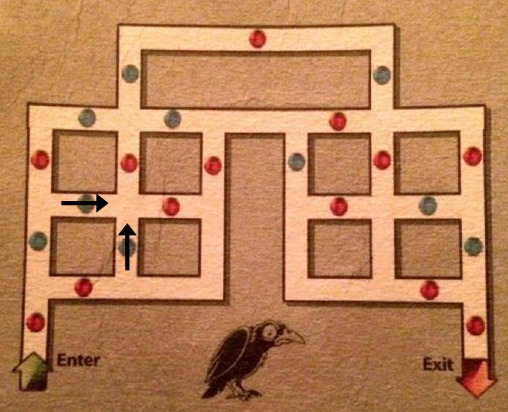
En este punto es importante detenernos: podemos decir que hemos reducido el problema de salir del laberinto, al problema de pasar por alguna de las dos esferas azules, en el sentido indicado por las flechas (ya que, si logramos esto, podremos salir siguiendo el camino que ya hemos trazado según el análisis anterior).

Dicho de otra forma: podemos dejar de lado por el momento el problema original. Hemos cambiado el problema de llegar desde un punto A a un punto C, por el problema de llegar desde A hasta un punto intermedio B (ya que sabemos cómo llegar luego desde B hasta C).

Análisis top-down

Esta estrategia («top-down», «descendente» o «de arriba hacia abajo») es la que nos resulta más natural e intuitiva: partir desde el comienzo y tratar de determinar los pasos subsiguientes, en el orden normal. Si comenzamos por la entrada del laberinto, veremos que (ya que debemos alternar los colores) los primeros cinco pasos son evidentes:

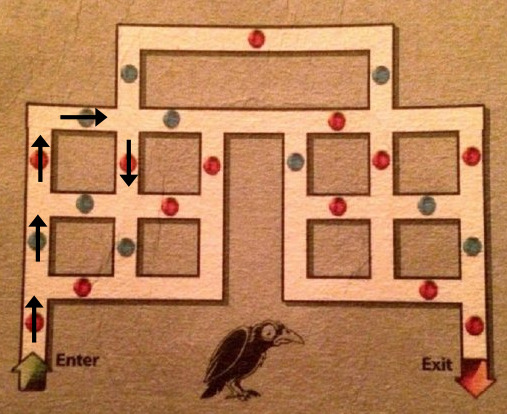
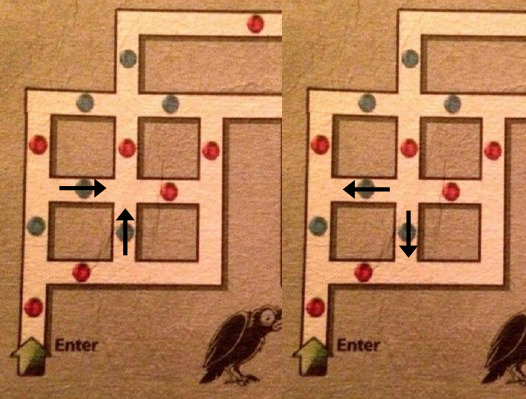
En este punto se nos presentan dos opciones para atravesar esferas azules:

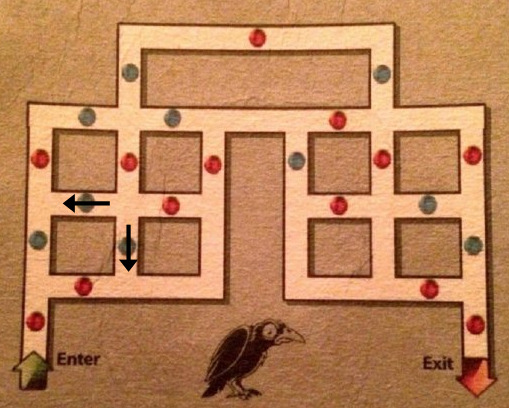
Y aquí, nos encontramos con una situación clave. Anteriormente habíamos reducido el problema a lograr pasar por alguna de estas dos esferas azules, pero en el sentido contrario al que llegaríamos al entrar al laberinto:

Un nuevo problema

En este punto, podemos formular un nuevo (sub) problema: invertir el sentido de circulación dentro del laberinto. Esto es, pasar por un lugar inicialmente en un sentido, y luego en otro. Por lo visto anteriormente, esta es la clave para resolver el problema inicial.

En este punto no parece haber estrategias para buscar una solución. Pero recorrer el laberinto (siempre considerando la alternancia de colores) para lograr cambiar el sentido de circulación es, sin dudas, un problema más simple que el original.

Sin demasiado esfuerzo, es bastante fácil encontrar la secuencia de pasos que permite lograr este (sub) objetivo:

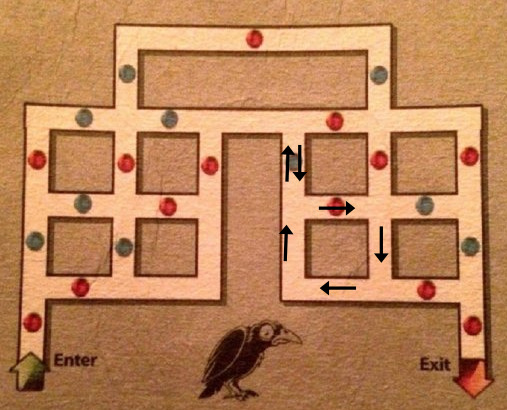
La solución

Reunamos los resultados de los tres análisis que hemos realizado hasta el momento.

Entrar al laberinto:

Invertir el sentido de circulación:

Salir del laberinto:

La solución es unir estos tres pasos. Algo realmente muy fácil de hacer. ¿Verdad?

El por qué de este artículo

El problema del laberinto es interesante, pero no es más que una excusa. El objetivo de este artículo fue mostrar como utilizando técnicas bastante sencillas y de forma metódica y ordenada (en vez de la forma intuitiva con la que la mayoría encara este tipo de problemas) puede encontrarse una solución sin requerir ningún tipo de «genialidad».

Este es apenas un ejemplo simple, pero sirve para ilustrar el tipo de recursos que se utilizan para la resolución algorítmica de problemas (el núcleo de las carreras relacionadas con la programación). Todos los años, miles de jóvenes se inscriben en carreras universitarias de computación pensando que aprenderán «todo» sobre computadoras, cuando en realidad su tarea se parece mucho más al tipo de análisis esbozado en este artículo. Uno de los pioneros de la programación, Edsger Dijkstra lo resumía diciendo que «la ciencia de la computación no trata sobre computadoras más de lo que la astronomía trata sobre telescopios».